[WGCNA] 유사도 네트워크 계산

CDeo 2024. 8. 14. 23:40

`[WGCNA] 기본개념`에서 이어지는 내용입니다.

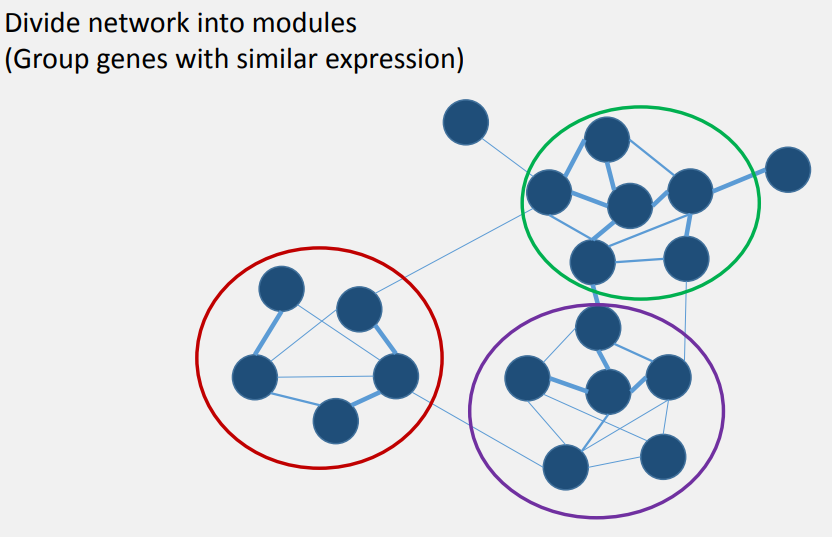
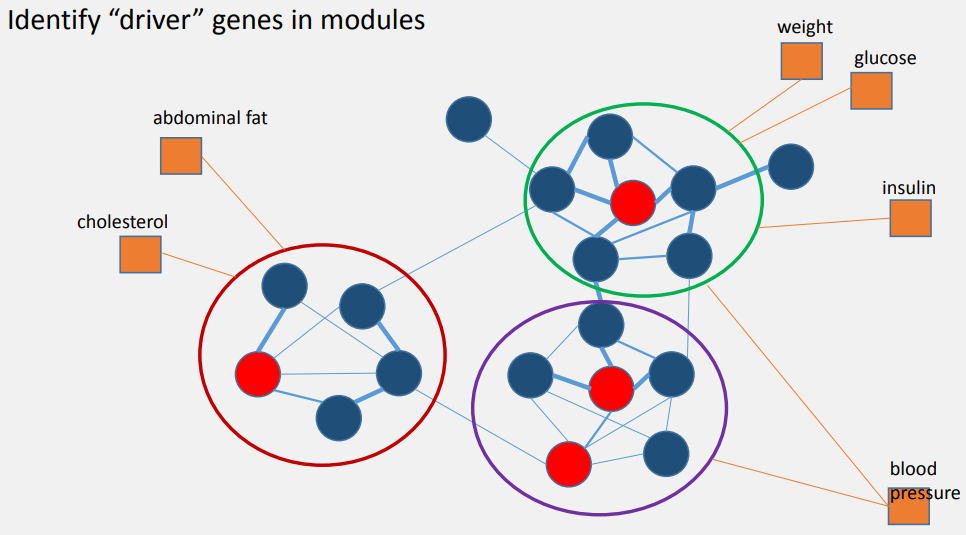
WGCNA는 크게 네가지 단계로 나누어집니다. 이번 포스팅에서는 그 첫번째 단계인 유전자의 유사도를 계산하는 단계에 대해 알아보겠습니다. 이번에 들여다볼 내용은 세부적으로 들어가면 계산 식과, 여러 종류의 계수를 선택해야 합니다만, 결국에는 딱 세가지 중요한 질문에 답하실 수 있으시면 됩니다: `1. 어떤 상황에 어떤 상관계수를 사용해야하는가?`, `2. 어떻게 최적의 β 를 잡을까?`, `3. 어떤 목적으로 어떤 네트워크를 사용해야 할까?`

이번의 설명은 널리 사용되는 WGCNA (R 라이브러리)를 기준으로 작성되었습니다.

Input data

우선, 주어지는 자료는 유전자 발현 행렬($X$)로 아래와 같이 표현 가능합니다. 여기서의 행은 유전자, 열은 샘플입니다.

$$X=[x_{ij}]=\left[ {\begin{array}{cc} \underline{x}_{1} \\ ... \\ \underline{x}_{n} \\ \end{array} } \right] \in \mathbb{R}^{n \times m}$$

$n$: # of network nodes (genes), $m$: # of sample

$i^{th}$ row vector: $\underline{x_i} \in \mathbb{R}^{1 \times m}$

Correlation

주어진 행렬에 대해 유사도는 아래와 같이 구할 수 있습니다.

$$s_{ij}=|cor(\underline{x}_i, \underline{x}_j)|$$

여러 종류의 유사도 중 골라 사용하면 됩니다만, WGCNA 논문과 일반적으로 사용되는 유사도는 아래 접은글에 정리해두었습니다.

Correlations for WGCNA

1. Pearson correlation

선형 상관 관계: 두 변수 간의 선형 관계를 측정합니다.
이상치에 민감함: 이상치(outliers)가 있을 경우 상관계수가 크게 왜곡될 수 있습니다.

2. Spearman, Kendall correlation

이상치에 robust함 : 이상치의 영향을 덜 받으며, 비선형적인 관계를 잘 포착할 수 있습니다.
비선형 상관 관계 포함: 두 변수 간의 단조(monotonic) 관계를 측정하며, 반드시 선형일 필요는 없습니다.
유전자 발현 차이에 덜 민감함: 유전자 발현 값의 절대적인 크기보다는 순위(rank)에 기초한 상관을 측정하기 때문에, 발현 차이에 덜 민감합니다.

3. Biweight midcorrelation

이상치에 매우 robust함: 이상치가 $med(x)$보다 $9mad(x)$ 이상 크면, 해당 이상치는 계산에서 제외되어 0으로 간주됩니다.
강력하게 이상치를 배제함으로써 다른 순위 기반 상관계수보다 더 강건한 상관관계를 측정할 수 있습니다.
저자 권장 방법: 특히 WGCNA 분석에서 이 방법이 권장됩니다, 이는 이상치에 대한 강건함과 함께 네트워크 분석에서 안정적인 상관관계 측정을 가능하게 하기 때문이라고 합니다.

이런 상관계수들이 주로 사용됩니다. 이중에서 biweight midcorrelation의 경우 해당 방법론에서 독자적으로 제시한 상관계수 입니다. 이에 대해서도 많은 설명 및 정리가 있습니다. 아래의 `html`은 나름 정리해둔 내용이니 참고 해주세요~!

Biweight midcorrelation.html

0.10MB

또한 상관계수의 선택은 전체적인 상황에 맞게 신중하게 이루어져야 합니다. 앞서 설명한 상관계수들의 특성을 이해한 후, 다음과 같은 Q&A를 통해 상황에 맞는 상관계수의 선택을 도울 수 있습니다.

Power term

유전자 사이의 관계는 거듭제곱 될 수 록 분명해집니다. WGCNA에서는 거듭제곱 항 $\beta$를 통해 분명함을 조절합니다.

$$a_{ij}=s_{ij}^{\beta}$$

조금 구체적으로는 강하고 약한 관계성에 대한 fold differences를 조절합니다. 예를들어,

$cor(\underline{x}_i, \underline{x}_j)=0.8$ & $cor(\underline{x}_k, \underline{x}_l)=0.2$

$\beta=4$ $→$ $0.8/0.2=4$ vs. $0.8^{4}/0.2^{4}=256$

$β$가 증가함에 따라 가중치 간의 차이가 커지게 되며, 이는 전체 그래프 연결성에서 더 뚜렷한 대조(laeger contrast)를 만들어냅니다. 그러나$β$ 값이 너무 커지면 작은 가중치들이 빠르게 0으로 수렴하게 되어 분석이 불가능해질 수 있습니다. 따라서 어느정도 대조를 보여 제법 클러스터링이 되는 "적절한" 네트워크를 찾기 위해서는 $β$ 값을 신중하게 선택해야 합니다. 이런 네트워크를 여기서는 스케일-프리 네트워크로 두는데, 이 작업은 일반적으로 $β$에 따른 스케일-프리 topology 모델의 R-제곱값(R-squared)과 평균 연결성(mean connectivity) 값을 분석하여 수행됩니다.

참고로 스케일-프레 네트워크는 랜덤한 연결성을 지닌 랜덤 네트워크와는 조금 다릅니다:

랜덤 네트워크: 모든 노드가 비슷한 수로 랜덤한 연결을 가질 확률이 높음
- 노드의 연결정도(degree)가 분포가 포아송 분포를 보임
스케일-프리 네트워크: 소수의 노드가 굉장히 많은 연결을 가지고, 대다수의 노드는 적은 연결을 갖음
- 노드의 degree 분포가 멱함수(power law) 분포를 보임

아래는 스케일-프리 네트워크의 $R^2$와 mean connectivity에 대한 간략한 설명과 $\beta$를 선택하는 방법에 대해 적어두었습니다.

I. $R^2$ 지수와 스케일-프리 네트워크 적합성 평가

스케일-프리 네트워크와 랜덤 네트워크는 노드 degree의 분포 특성에서 명확히 구분됩니다. 스케일-프리 네트워크는 power-law분포, 랜덤 네트워크는 포아송분포를 따릅니다. 따라서, 네트워크의 구조적 특성을 파악하기 위해서는 이 두 분포를 구별하는 것이 핵심입니다.

노드 degree 분포에 로그 변환을 적용하면, power-law 분포는 로그-로그 스케일에서 선형적인 관계로 나타납니다. 이를 통해 스케일-프리 특성을 직관적으로 확인할 수 있습니다. 하지만 포아송 분포 역시 로그-로그 스케일에서 선형적인 형태를 일부 나타낼 수 있기 때문에, 단순한 시각적 판단만으로는 정확한 판별이 어렵습니다.

이러한 한계를 보완하기 위해, 로그 변환된 degree 분포 $log(p(k))$와 $log(k)$ 사이에 **선형 회귀(linear regression)**를 수행하고, 그 결정계수 $R^2$ 를 계산함으로써 스케일-프리 특성의 정량적 적합도를 평가할 수 있습니다. 일반적으로 $R^2$ 값이 높을수록 해당 네트워크가 power-law 분포를 잘 따르고 있음을 의미합니다.

랜덤 네트워크에 대해 가정한 포아송 분포와 스케일 프리 네트워크에 대해 가정한 power law 분포에 대해 간단히 로그 변환을 통해 스케일 프리 정도를 결정계수로 비교해본 R `html` 입니다.

Scalefree_R.html

0.71MB

일반적으로 power law 분포에 대해 적합한 회귀 모형의 결정계수 값이 큽니다.

이를 이용한 세 가지 유전자 공발현(gene co-expression) 네트워크 분포 모델은 다음과 같습니다:

Barabasi (1999), 스케일-프리 모델
- $log(p(k))=c_0+c_1log(k)$
- 이 모델은 단순한 스케일-프리 네트워크를 설명하며, 노드의 연결 정도가 power-law 법칙을 따릅니다.
Csanyi-Szendroi (2004), 지수적으로 절단된 스케일-프리 토폴로지 (Exponentially Truncated SFT)
- $log(p(k))=c_0+c_1log(k)+c_2k$
- 이 모델은 스케일-프리 네트워크에 지수적 절단면을 추가하여, 네트워크 내에서 연결 정도의 분포가 급격히 감소하는 현상을 설명합니다.
Horvath, Dong (2005), 로그 로그 스케일-프리 토폴로지 (Log Log SFT)
- $log(p(k))=c_0+c_1log(k)+c_2log(log(k))$
- 이 모델은 스케일-프리 네트워크를 보다 정밀하게 설명하며, 이중 로그 변환을 통해 분포의 특성을 설명합니다.

이러한 모델들은 유전자 공발현 네트워크의 분포를 적절히 설명하며, 각 모델의 적합성을 평가할 때 $R^2$ 지수를 사용하여 네트워크의 적합도를 확인할 수 있습니다. $R^2$ 지수가 높을수록, 해당 모델이 주어진 데이터에 잘 맞는다는 것을 의미합니다.

II. Connectivity index

Connectivity Index는 네트워크에서 특정 유전자의 연결성을 측정하는 지표로, 해당 유전자와 연결된 모든 엣지의 가중치 합으로 정의됩니다. 수식으로 표현하면, 유전자 $의 연결성(Connectivity) $k_i$는 다음과 같이 계산됩니다:

$k_i=\sum a_{ij}$

이 연결성 지표는 유전자 네트워크 분석에서 중요한 역할을 하며, 유전자의 중심성(centrality)을 평가하거나 네트워크 내에서 유전자 간의 상호작용 강도를 측정하는 데 사용됩니다. 연결성 지수가 높을수록 해당 유전자가 네트워크 내에서 중요한 역할을 할 가능성이 큽니다.

III. $\beta$ 선택

먼저, 하이퍼파라미터 최적화 방법 중에서 Grid Search는 주어진 범위 내에서 하이퍼파라미터의 조합을 체계적으로 탐색하는 방법입니다. 주어진 범위가 명확히 정의되어 있는 경우, Grid Search는 충분히 적용 가능한 방법입니다. 이 방법을 통해 최적의 하이퍼파라미터 조합을 찾아낼 수 있습니다.

이를 통해 네트워크의 스케일-프리 특성의 질과 전체 네트워크의 평균 연결성이 "뚜렷한" 네트워크의 지표가 된다는 것을 알 수 있습니다. 즉, 적절한 $β$ 값은 네트워크의 스케일-프리 구조를 잘 반영하면서도 연결성을 유지할 수 있는 값이어야 합니다.

Networks

네트워크를 구성할 때, 각 유전자 간의 연결성(연결 가중치)은 인접 행렬(adjacency matrix)의 요소인 $a_{ij}$로 표현됩니다. 이 가중치 $a_{ij}$ 는 유전자 $i$와 $j$ 사이의 엣지의 강도를 나타내며, 네트워크 유형에 따라 계산 방법이 달라집니다. 주로 사용되는 네트워크 유형 Unsigned, Signed, Signed hybrid Network 총 세가지로 나뉩니다. 디테일한 내용은 아래에 접어두었습니다.

1. Unsigned Network (default)

연결 가중치 계산:

$$a_{ij}=|cor(\underline{x}_i, \underline{x}_j)|^{\beta}$$

여기서 $\text{cor}(x_i, x_j)$는 유전자 $i$와 $j$사이의 상관계수입니다.
특징: 양의 상관관계와 음의 상관관계의 차이를 두지 않고 절대값을 취하여 가중치를 계산합니다.
사용 경우: 음의 상관관계 분석에 포함할 때 적합합니다. 즉, 두 유전자 간의 발현이 반대 방향으로 변화하더라도 이 정보를 중요하게 고려할 때 사용됩니다.

2. Signed Network

연결 가중치 계산:

$$a_{ij}=({1+cor(x_i, x_j)\over{2}})^{\beta}$$

특징: 양의 상관관계와 음의 상관관계가 명확히 구분됩니다. 양의 상관관계만 네트워크에 반영되며, 음의 상관관계는 연결이 없는 것으로 간주됩니다.
사용 경우: 유전자 발현 패턴의 방향성을 고려할 때 유용합니다. 즉, 두 유전자가 함께 증가하거나 감소할 때만 연결로 간주됩니다.

3. Signed Hybrid Network

연결 가중치 계산:

for $\text{cor}(x_i, x_j) > 0$

$$a_{ij}=|cor(\underline{x}_i, \underline{x}_j)|^{\beta}$$

for $o.w$

$$a_{ij} = 0$$

특징: 양의 상관관계만 고려되며, 음의 상관관계는 0으로 처리됩니다. 이는 음의 상관관계를 완전히 배제하고자 할 때 사용됩니다.
사용 경우: 음의 상관관계가 분석에 포함되지 않도록 하고, 양의 상관관계만 중요한 경우에 적합합니다. 이 방법은 일반적으로 Signed Network보다 더 작은 $\beta$ 값을 사용할 수 있습니다.

네트워크 유형 선택에 대한 고려사항

Signed? Unsigned?

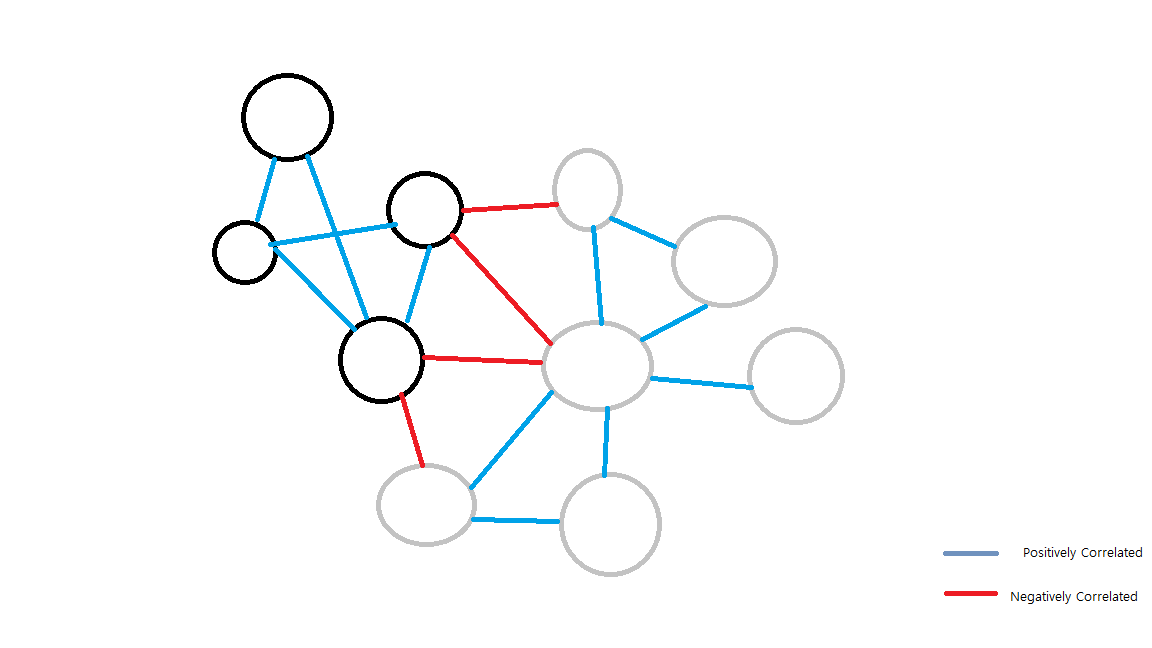
(Middle) Module with Unsigned Network & (Right) Modules with Signed Network

Unsigned vs. Signed: 음의 상관관계를 포함하고 싶다면 Unsigned Network를 사용하는 것이 좋습니다. 예를 들어, 약물 처리 후에 유전자가 반대로 발현되는 패턴을 찾고자 할 때, 음의 상관관계를 포함하지 않으면 중요한 정보를 놓칠 수 있습니다. 하지만, 양의 상관관계만을 중심으로 해석 가능성을 높이고자 한다면 Signed Network를 선택할 수 있습니다. (논의 링크)
Signed vs. Signed Hybrid: Signed Network는 방향성을 고려하지만, Signed Hybrid는 연결성을 보다 엄격하게 관리하며 음의 상관관계를 완전히 배제합니다. 적절한 $\beta$ 값을 선택하는 데 있어 Signed Hybrid가 더 작은 값을 사용할 수 있어 유리할 수 있습니다. (논의 링크)