[머피 책] Chapter 1 #2

머피 책 공부하면서 새롭게 알게된 사실 또는 궁금한 부분에 대한 기록입니다.

---

Voronoi Tessellation

기하학에서 주어진 점 집합을 기반으로 공간을 분할하는 기법입니다. 머피 책에서 `knn` 알고리즘에서 $k=1$인 경우의 분류 방식이, 본질적으로 `Voronoi tessellation`으로 영역을 분할하는 방식과 같다고 합니다. 이러한 맥락으로 책에 등장한 개념인데, 먼저 `Voronoi tessellation`은 만드는 방법이 아주 간단합니다. 가장 가까운 두 점들을 모두 연결한 뒤, 그 선들을 수직 이등분하며 영역을 분할하는 방식입니다. 분할 된 영역에 새로운 데이터가 들어가면, 그 나뉘어진 영역을 차지하고 있는 그 점과 같은 클래스로 분류되며, 이는 최근접 이웃 하나를 기준으로 분류되는 `knn` 알고리즘에서 $k=1$의 경우와 같습니다.

이 방법은 `Delaunay triangulation`와 쌍대 관계에 있기도 합니다.

Delaunay triangulation

Delaunay triangulation은 각 점들을 이어 삼각형의 모양으로 면을 분할하는 방법입니다. 방법의 핵심은 점 세개를 정하여 삼각형을 만듦에 있어 어떤 다른 점도 내부에 포함하지 않으며 내각의 최솟값이 최대가 되도록, 쉽게 말하자면 최대한 정삼각형에 가깝도록 하는것에 있습니다. 이 방법은 각 점들을 삼각형으로 이으면, 적어도 Convex Hull 내부는 전부 빠짐없이 분할된다는 아이디어가 돋보이는 분할법 으로 보입니다.

Delaunay triangulation에 의하면 (b)가 (c)보다 더 잘 나뉘었다.

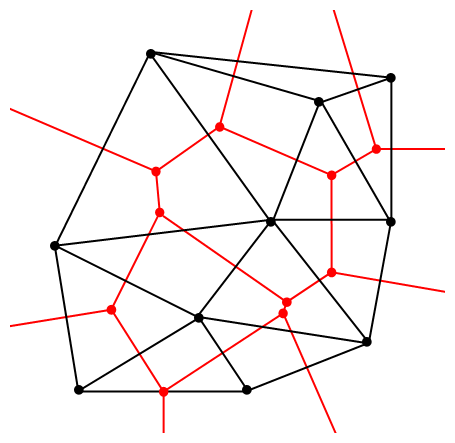
Delaunay triangulation에서 얻은 삼각형의 외심이 결국 삼각형의 각 변의 수직 이등분선이 만나는 지점이다보니, 그 외심을 꼭지점으로 하는 다각형이 생기며, 이를 직선으로 이어 Voronoi tessellation을 만들수 있게 됩니다.

(검정) Delaunay (빨강) Voronoi

참고로, 잠자리나, 기린에서 많이 보이는 패턴이라고 합니다.

References

Wiki

https://teamhoudini.wordpress.com/2018/12/06/camilla-voronoi-diagram-knowledge-analysis-in-nature/

Camilla: Voronoi Diagram Knowledge Analysis: In nature

https://hpaulkeeler.com/voronoi-dirichlet-tessellations/

Voronoi tessellations – H. Paul Keeler