[7월] 하늘 위의 숨겨진 네트워크: 항공편의 어쩌면 재미있는 비밀

여러분, 비행기를 타본 적 있으신가요? 오늘은 공항과 비행 항로가 만드는 놀라운 네트워크의 세계로 여러분을 초대합니다. 이 네트워크에는 우리가 미처 몰랐던 흥미로운 비밀이 숨어있답니다!

🌎 지구를 감싸는 비행 네트워크

전 세계의 공항과 비행 경로를 하나의 거대한 네트워크로 상상해보세요. 이 네트워크는 수학적으로 그래프로 모델링할 수 있어요. 공항은 노드(점)가 되고, 비행 경로는 엣지(선)가 되죠. 

흥미로운 점은, 이 네트워크가 단순히 무작위로 연결된 랜덤 네트워크가 아니라는 거예요. 현실 세계의 많은 네트워크처럼, 비행 네트워크도 어떠한 특성을 지닌  '스케일 프리 네트워크'의 형태를 보입니다. 

🧠 랜덤 vs 스케일 프리

• 랜덤 네트워크: 모든 노드가 비슷한 수로 랜덤한 연결을 가질 확률이 높아요.
• 스케일 프리 네트워크: 소수의 노드가 굉장히 많은 연결을 가지고, 대다수의 노드는 적은 연결을 가져요.

우리의 비행 네트워크가 스케일 프리인 이유는 뭘까요? 바로 현실 세계의 자연스러운 발전 과정 때문이에요. 큰 도시에 더 많은 항로가 생기고, 이는 다시 그 도시를 더 중요한 허브로 만들죠. 이런 부자가 더 부자가 되는 과정이 스케일 프리 네트워크를 만들어 냅니다.
 
그렇다면 과연 실제 세상에서 이런 양상을 정말로 보일지 OpenFlights 데이터셋을 통해 살펴보려고 해요!

import pandas as pd
import networkx as nx
import matplotlib.pyplot as plt
import requests

# OpenFlights data set URL
url_routes = '<https://raw.githubusercontent.com/jpatokal/openflights/master/data/routes.dat>'

# data download
routes_response = requests.get(url_routes)

# save
with open('routes.dat', 'wb') as file:
    file.write(routes_response.content)

# load
columns_routes = ['Airline', 'AirlineID', 'SourceAirport', 'SourceAirportID', 'DestinationAirport', 'DestinationAirportID', 'Codeshare', 'Stops', 'Equipment']
routes = pd.read_csv('routes.dat', header=None, names=columns_routes, dtype={'SourceAirport': str, 'DestinationAirport': str})

# graph
G = nx.from_pandas_edgelist(routes, source='SourceAirport', target='DestinationAirport')

# graph visualization
plt.figure(figsize=(12, 8))
nx.draw(G, with_labels=False, node_color='skyblue', node_size=1, edge_color='gray')
plt.title("Airline Network Graph")
plt.show()

이 그래프를 자세히 보면, 소수의 큰 허브 공항과 다수의 작은 공항들이 어떻게 연결되어 있는지 한눈에 볼 수 있어요. 이것이 바로 스케일 프리 네트워크의 특징이죠!

✈️ 허브 공항의 마법

스케일 프리 네트워크의 가장 흥미로운 특징은 '허브'의 존재입니다. 비행 네트워크에서 이는 바로 대형 허브 공항들이죠. 대부분의 공항은 연결된 항로가 몇 개 없지만, 소수의 허브 공항들은 수백 개의 항로와 연결되어 있습니다.
 
이런 허브의 존재는 네트워크의 '직경'에 큰 영향을 미칩니다. 여기서 직경이란 네트워크에서 가장 멀리 떨어진 두 노드 사이의 최단 경로를 의미해요. 허브 덕분에 이 직경이 놀랍도록 짧아집니다!
 
예를 들어, 여러분이 작은 지방 공항에서 출발해 지구 반대편의 또 다른 작은 공항으로 가려면 대개 2~3번의 경유만으로 충분합니다. 첫 번째 비행으로 허브 공항에 도착하고, 거기서 다른 허브로, 그리고 마지막으로 목적지로 가는 식이죠.
 
이런 현상을 네트워크 과학에서는 "작은 세상 효과"라고 부릅니다. 그래서 우리는 종종 허브에서 아는사람을 우연히 만나며 "세상 참 좁다!"라고 말하게 되는 거예요. 허브 공항들이 세상을 더 작고 연결된 곳으로 만들어주는 마법 같은 역할을 하는 셈이죠.
 
이런 구조가 전 세계를 놀랍도록 효율적으로 연결하는 비결입니다. 허브 덕분에 우리는 지구 어느 곳이든 빠르게 갈 수 있게 된 거예요!

🎭 평균의 함정

비행 네트워크의 데이터를 자세히 들여다보면, 스케일 프리 네트워크의 흥미로운  통계적인 패턴을 찾을 수 있습니다. 이 자료에 따르면, 전 세계에는 총 3425개의 공항이 있고, 공항당 평균 연결 항로 수는 약 11개입니다. 하지만 이 '평균'이 현실을 얼마나 잘 반영할까요? 놀랍게도, 전체 공항 중 단 43개(1.3%)만이 이 평균의 연결을 가지고 있어요!

📏 '스케일'의 의미

 

여기서 '스케일'이란 노드 연결 정도(degree)의 평균값을 의미해요. 일반적인 랜덤 네트워크에서는 대부분의 노드가 이 평균값 근처의 연결 수를 가집니다. 예를 들어, 평균 연결 수가 7이라면, 대부분의 노드가 7개 정도의 연결을 가지는 거죠.

 

일반적으로 임의로 노드를 관찰할 때, 우리는 해당 노드에서 평균적인 연결 정도를 기대합니다. 하지만, 스케일 프리네트워크는 위의 보기와 같이 임의로 잡은 노드에게서 평균 값인 스케일을 기대할 수 없죠! 때문에 scale이 정해지지 않은 (free) 스케일 프리라는 이름을 갖게 된 것입니다. 이름 참 잘 지었죠? 뒤에 설명할 "분산의 발산" 과도 연관이 있습니다.

더 놀라운 사실을 보여드릴게요:

• 전체 공항의 약 80%(2723개)는 10개 이하의 연결 항로를 가집니다.
• 반면, 상위 10개 허브 공항의 평균 연결 항로 수는 무려 217개!

degree_sequence = sorted([d for n, d in G.degree()], reverse=True)
print("The number of airports: ", len(degree_sequence))
print("Mean number of the edges: ", np.mean(degree_sequence))
print("The number of airports with 11 edges: ", sum(1 for edge in degree_sequence if edge == 11))
print("The number of airports with fewer than 10 edges: ", sum(1 for edge in degree_sequence if edge <= 10))
print("Mean of top 10 edges : ", np.mean(sorted(degree_sequence, reverse=True)[:10]))

The number of airports:  3425
Mean number of the edges:  11.244963503649634
The number of airports with 11 edges:  43
The number of airports with fewer than 10 edges:  2723
Mean of top 10 edges :  216.8

이런 극단적인 차이가 바로 스케일 프리 네트워크의 특징적인 긴 꼬리분포 형태의 'power law' 분포를 만들어냅니다.

# distribution of degrees
plt.hist(degree_sequence, bins='auto', color='skyblue', alpha=0.7, rwidth=0.85)
plt.title("Degree Histogram")
plt.xlabel("Degree")
plt.ylabel("Count")
plt.show()

 

이 히스토그램을 보세요. 왼쪽에 대부분의 공항이 몰려있고(적은 연결), 오른쪽으로 길게 뻗은 꼬리 부분에 소수의 허브 공항들이 자리잡고 있습니다. 이것이 바로 'power law' 분포의 모습이에요.

🎡 분산의 발산

이런 극단적인 차이가 나타나는 현상에 대해 통계학에서 '분산의 발산'으로 설명하기도 합니다. 쉽게 말해, 허브 공항과 작은 공항의 차이가 너무 커서 평균이나 분산 같은 전통적인 통계 척도가 의미를 잃어버리는 거죠.

(증명) Power law distribution; 분산의 발산

예를 들어, 평균 연결 수 11개는 실제로 대부분의 공항(80%가 10개 이하!)과 동떨어진 수치입니다. 반면 상위 10개 공항의 평균 연결 수 217개는 이 평균의 무려 20배에 달하죠.

🧠 왜 이게 중요할까?

1. 효율적인 여행: 소수의 대형 허브를 통해 전 세계가 긴밀히 연결됩니다. 작은 공항에서 출발하더라도, 허브를 거쳐 빠르게 목적지에 도착할 수 있어요.
2. 네트워크 강건성과 취약성: 80%의 작은 공항에 문제가 생겨도 네트워크는 크게 영향받지 않습니다. 하지만 상위 10개 허브 중 하나라도 문제가 생기면? 전체 네트워크가 크게 흔들릴 수 있어요.
3. 비즈니스 전략: 항공사들은 이런 구조를 활용해 효율적인 '허브-앤-스포크' 전략을 구사합니다.
4. 현실 이해: '평균'만으로는 실제 네트워크의 모습을 이해하기 어렵다는 것을 알 수 있어요. 복잡한 시스템을 이해하려면 더 깊이 들여다봐야 합니다.

🌈 마무리

다음에 비행기를 탈 때, 이런 생각을 해보세요: "내가 지금 있는 이 공항은 저 80%에 속하는 작은 공항일까, 아니면 상위 10개 허브 중 하나일까?" 그리고 기억하세요, 이런 불균형한 구조가 오히려 우리 세상을 더 효율적으로 연결하는 비결이라는 걸요!

🧬 스케일 프리, 그 너머의 세계

재미있는 사실은, 이런 스케일 프리 네트워크의 특성이 비행 네트워크에만 국한되지 않는다는 거예요. 제가 처음 이 개념을 마주친 것은 사실 유전자 네트워크를 분석하면서였답니다. 주요 허브 공항이 존재하듯, 생물학에서도 주요한 '허브 유전자'가 존재한다는 사실! 놀랍지 않나요?
 
더 깊이 들어가보면, 해당 네트워크가 과연 스케일 프리인지 확인하는, 결정계수 기반의 정량적 평가 기법도 여럿 존재한답니다.

- 정량적 평가 기법

1. Barabasi (1999), Scale Free
   • $log(p(k))=c_0+c_1log(k)$
2. Csanyi-Szendroi (2004), Exponentially Truncated SFT
   • $log(p(k))=c_0+c_1log(k)+c_2k$
3. Horvath, Dong (2005), Log Log SFT
   • $log(p(k))=c_0+c_1log(k)+c_2log(log(k))$

 

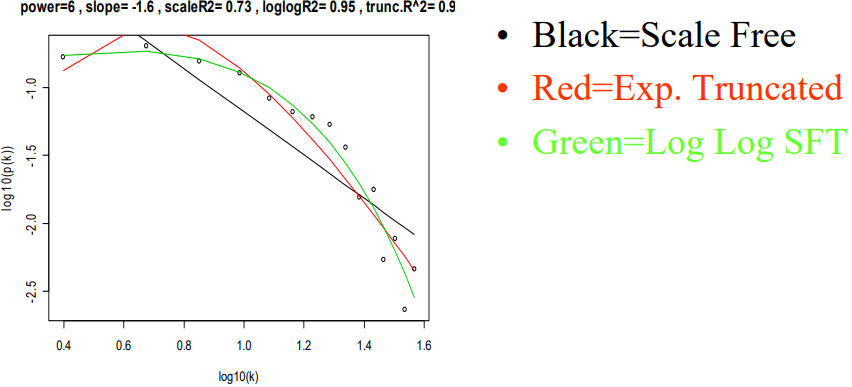
랜덤 네트워크에 대해 가정한 포아송 분포와 스케일 프리 네트워크에 대해 가정한 power law 분포에 대해 간단히 로그 변환을 통해 스케일 프리 정도를 결정계수로 비교해본 R html. 일반적으로 power law 분포에 대해 적합한 회귀 모형의 결정계수 값이 크다.

Scalefree_R.html

0.71MB

거기에 더하여, 이런 구조가 시간이 지남에 따라 어떻게 형성되는지도 흥미롭습니다. 마치 "부자가 더 부자가 되는" 현상처럼, 허브는 점점 더 많은 연결을 얻게 되죠. 이는 군집화 알고리즘에서도 비슷한 원리로 활용되가도 합니다.
 
예를 들어, 마코브 클러스터링이라는 방법은 이런 원리를 이용해요. 처리를 반복할수록 유전자 사이의 강한 관계는 더 강해지고, 약한 관계는 더 약해지면서 자연스럽게 클러스터가 형성되는 거죠. 마치 시간이 지날수록 허브 공항이 더 큰 허브가 되는 것과 비슷하답니다.

📚 더 알아보기

스케일 프리 네트워크는 정말 다양한 분야에서 발견됩니다. 인터넷의 구조, SNS, 단백질 및 유전자 상호작용 네트워크 등등... 우리 주변의 많은 복잡한 시스템들이 이런 구조를 가지고 있어요.
 
여러분의 특별한 비행 경험이나 가장 좋아하는 허브 공항에 대해 댓글로 알려주세요! 어쩌면 그 경험 속에서 스케일 프리 네트워크의 흔적을 발견할 수 있을지도 모릅니다. 그리고 혹시 다른 분야에서 비슷한 패턴을 발견하셨다면, 그것도 함께 공유해주세요! 🛫🧬💡
 
이 주제에 대해 더 알고 싶으시다면, 네트워크 과학, 시스템 생물학 등의 키워드로 (영어로) 검색해보시는 것을 추천드립니다. 새롭고 재미있는 세계가 여러분을 기다릴수도?!
 

ℹ️ 참조

“The New Science of Networks”, Barabasi & Frango 2002
https://github.com/jpatokal/openflights?tab=readme-ov-file

GitHub - jpatokal/openflights: Website for storing flight information, rendering paths on a zoomable world map and calculating s