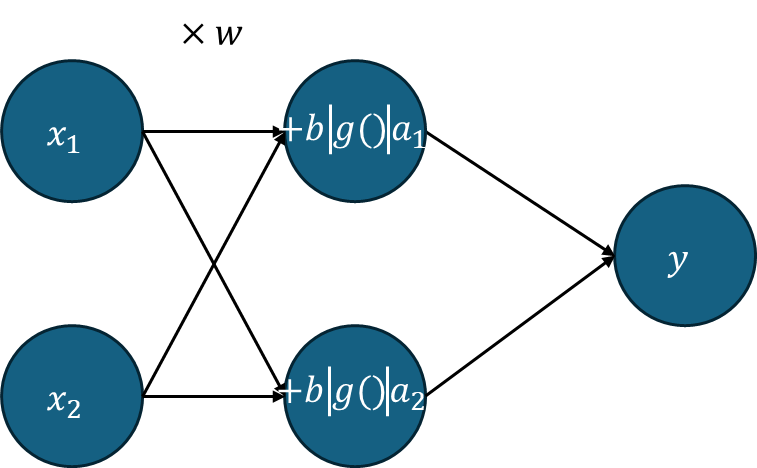[ML with JAX] XOR 분류기

이번 시리즈에서는 `JAX`의 문법을 정리하지는 않을예정입니다. `JAX`에 대해 정리해둔 내용은 아래의 내용을 확인해주세요!

https://hello-world-jhyu95.tistory.com/entry/JAX-Quick-Start

[JAX] Quick Start

대신 알고리즘들에 대한 개인적인 복습도 할 겸 `JAX`로 기본적인 머신러닝 기법들을 돌려보는 작업을 해보려합니다.

그런데 이번 포스터에서는 `JAX`를 쓸 구석이 안보이네요...ㅎㅎ;; 

---

Perceptron

먼저, 퍼셉트론이란 신경망의 구조에서 차용한 원시적인 분류기로, 딥러닝의 기초개념입니다. 이 개념은 여러 함수에 대한 표현이 될 수 있으며, 특히 시각화 방식이 유용하다 생각합니다. 예를들어, 어떤 로지스틱 회귀에 대한 식 $g(x_1w_1+x_2w_2+b)=y$를 아래와 같이 시각화가 가능합니다.

여기서 $g()$는 logit link function으로 딥러닝에서는 주로 sigmoid function이라고 불립니다. 이번 포스팅에서 등장하는 함수 $g()$는 그냥 결과를 종합해주는 (보통은 비선형성을 추가해주는 활성화) 함수 라고 생각해주시면 됩니다.

Logical operation

그렇다면, 이 퍼셉트론을 통해 어떤 문제를 해결 할수 있을까요? AND, OR, XOR 이진 논리연산에 대한 분류가 가능해집니다. 먼저 게이트에 대한 논리연산 결과는 다음과 같습니다.

AND			OR			XOR
$x_1$	$x_2$	$y$	$x_1$	$x_2$	$y$	$x_1$	$x_2$	$y$
0	0	0	0	0	0	0	0	0
0	1	0	0	1	1	0	1	1
1	0	0	1	0	1	1	0	1
1	1	1	1	1	1	1	1	0

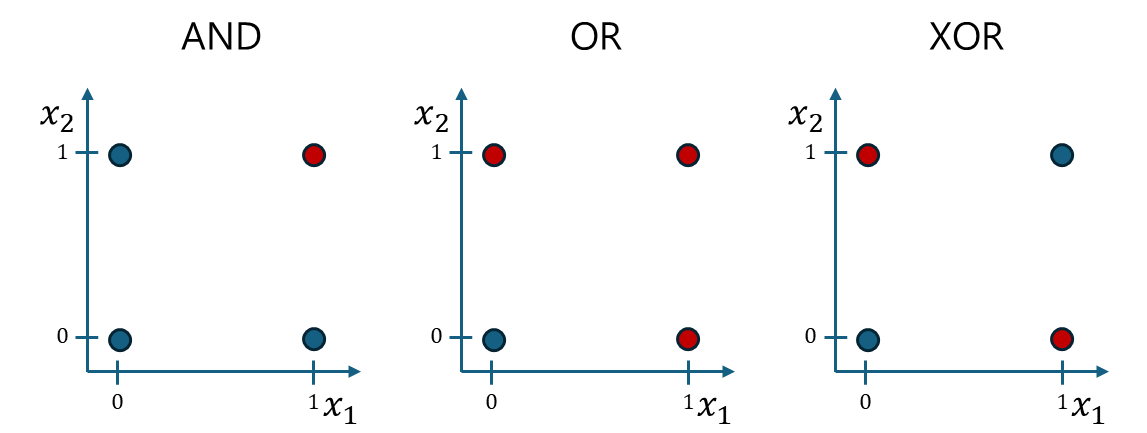
이를 그래프로 나타내면,

푸른 점: 0 / 붉은 점: 1

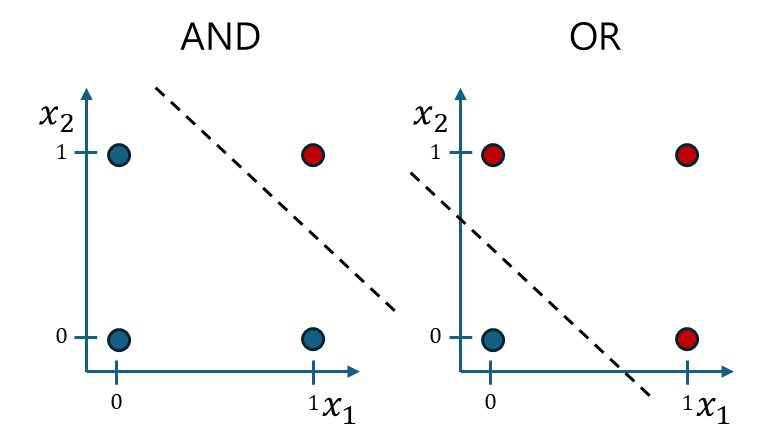
이런 형태가 됩니다. 여기서 AND와 OR의 경우에는 아래와 같이 `직선` 하나로 분류가 가능합니다.

적당한 기울기와 절편이 있는 일차함수로 해결됩니다. AND의 경우에는 기울기($w$)가 -1, y절편($b$)이 1.5 정도면 적당해보입니다. 그리고 OR의 경우에는 $w$가 -1, $b$가 0.5 정도면 적당해보입니다.

$$x_2=-x_1+b$$

$$x_2+x_1=+b$$

수식의 관점에서 본다면, 한 점의 특성인 $x_1$과 $x_2$의 합이 각각 b값인 1.5와 0.5 보다만 작으면 (또는 크면) 0 (또는 1)로 분류되도록 한다는 의미입니다. 퍼셉트론으로 보자면 다음과 같이 시각화가 가능합니다:

 

구현하자면 아래와 같습니다:

AND

def AND(x1, x2):
    w, b = -1, 1.5
    return 0 if x2 - x1*w < b else 1

X = [(0,0), (0,1), (1,0), (1,1)]
results = [AND(x1, x2) for x1, x2 in X]

results
>>> [0, 0, 0, 1]

OR

def OR(x1, x2):
    w, b = -1, 0.5
    return 0 if x2 - x1*w < b else 1

X = [(0,0), (0,1), (1,0), (1,1)]
results = [OR(x1, x2) for x1, x2 in X]

results
>>>[0, 1, 1, 1]

XOR

XOR의 경우에는 직선을 통한 분류가 불가능한 구조입니다만, 위의 두 연산을 적절히 사용한다면 분류가 가능해집니다. 바로 NAND(Not AND) 와 OR을 사용하는 것입니다.

($x_1$, $x_2$)	NAND($x_1$, $x_2$); $a_1$	OR($x_1$, $x_2$); $a_2$	AND($a_1$, $a_2$); $y$
(0,0)	1	0	0
(0,1)	1	1	1
(1,0)	1	1	1
(1,1)	0	1	0

 

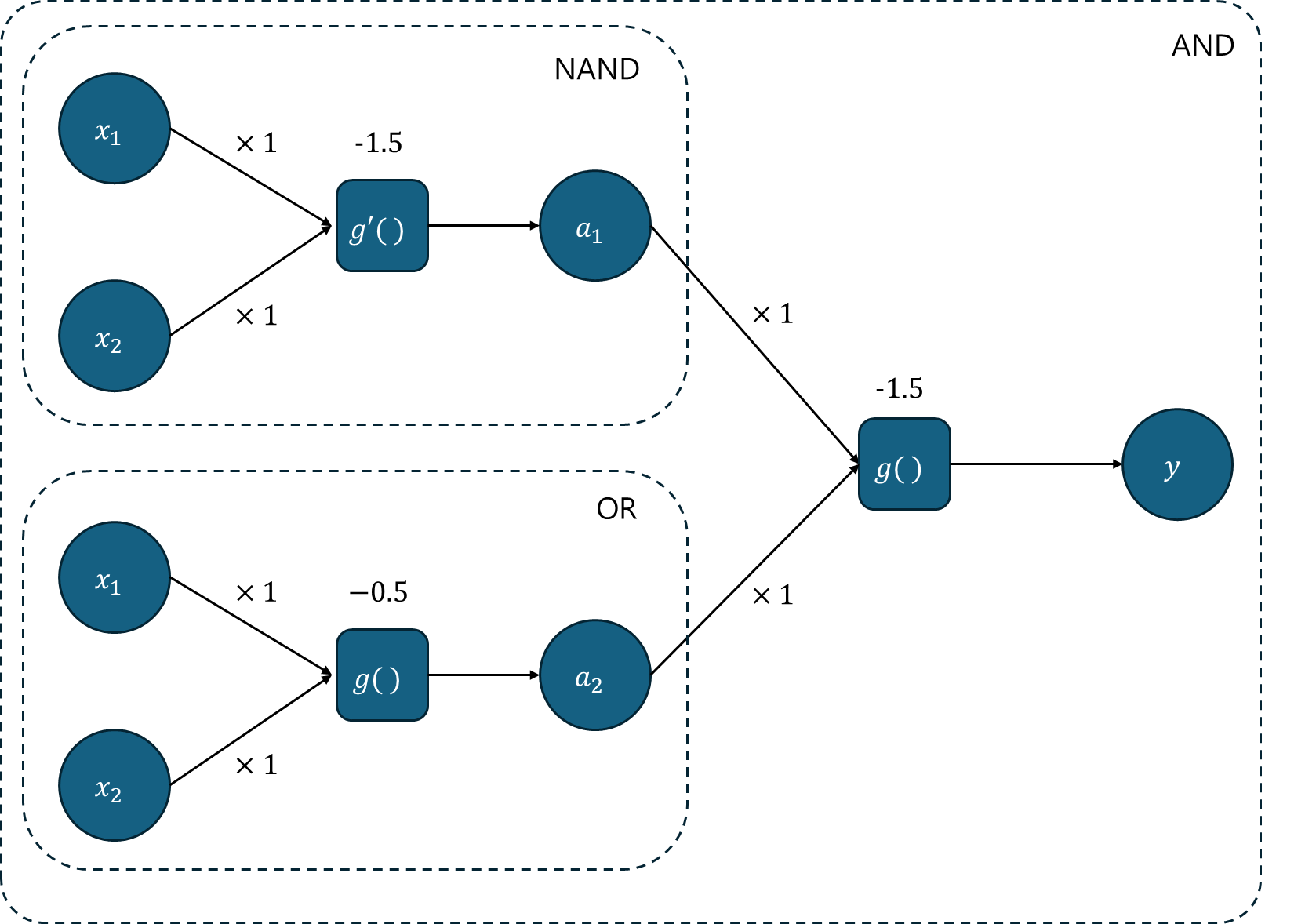
제가 표현력이 부족하여 2차원 평면에서는 나타내지 못하였지만, 퍼셉트론에 대한 표현으로는 아래와 같이 가능합니다:

(참고로  NAND구현 시에는 $w$와 $b$가 AND와 같지만, 그 부등호의 방향만 다르면 됩니다.)

def NAND(x1, x2):
    w, b = -1, 1.5
    return 0 if x2 - x1*w > b else 1

X = [(0,0), (0,1), (1,0), (1,1)]
results = [NAND(x1, x2) for x1, x2 in X]

results
>>>[1, 1, 1, 0]

결국 XOR은 아래와 같이 나타낼 수 있습니다.

def XOR(x1, x2):
    a1 = NAND(x1, x2)
    a2 = OR(x1, x2)
    return AND(a1, a2)
    
X = [(0,0), (0,1), (1,0), (1,1)]
results = [XOR(x1, x2) for x1, x2 in X]

results
>>>[0, 1, 1, 0]

Multi Layer Perceptron

이를 통해 알 수 있는 사실은, `직선`으로 분류가 불가능한 상황은 그 `조합`으로 해결 가능하다는 것입니다. 그림으로 간단히 그리자면 아래와 같습니다. 퍼셉트론을 한 층 쌓은듯한 느낌이죠? 

 

이러한 방식을 다중 층 퍼셉트론 (MLP) 라고 합니다. 이 층의 수를 늘려 직선으로는 분류 불가능한 `비선형` 문제에 도전할 수 있게 됩니다. 이는 사실 곡선을 그려 (간단하게, Quadratic form 또는 그 이상) 해결 가능한 방법이 있지만, 여기에서는 퍼셉트론과 활성화 함수의 중첩을 통해 문제를 해결했습니다.