Linear Discriminant Analysis
`Linear Discriminant Analysis (LDA)`는 분류와 차원축소에 사용되는 기법 중 하나입니다. 차원축소에 있어 LDA는 정사영(행렬 분해)을 통해 차원을 축소한다는 점에서 Principal Component Analysis (PCA)와 비슷하지만, 그 방향은 다소 다릅니다. PCA는 원본 데이터의 분산을 최대화하는 벡터를 찾고, LDA는 클래스 정보를 분할하기에 적합한 벡터를 찾아냅니다. 또한 분류 문제에서의 LDA는 지도학습의 일종으로, 두가지 클래스를 가장 잘 나누는 초평면을 구하는 방법으로 사용됩니다. 이 처럼 `LDA`는 결정경계의 추정, 분류 문제, 단순 차원축소등 활용가능한 범위가 넓습니다.

Objectives
Classification
먼저, `LDA`의 분석 목적이 분류라면 클래스간의 `선형 경계`를 찾는것이 알고리즘의 핵심입니다. 먼저 경계를 찾기위해 각 클래스의 확률 밀도함수를 사용합니다. 여기서 식을 단순히 전개하기에 그리고 자연계에서 자주 나타나기에, 가장 적절한 분포는 `다변량 정규 분포 (가정 1)`입니다. 이 분포를 통해 모델링을 하게되면 경계가 나오는데, `클래스마다의 공분산이 동일 (가정 2)`한 경우 그 경계가 `선형`이 됩니다. 가정이 두개지요.

그렇다면 이러한 가정 하에 LDA는 어떻게 경계를 구하는지 자세히 알아보겠습니다.
먼저 입력 $x$에 대해 class $k$에 속할 `(사후)확률`을 $P(G = k | X = x)$라고 한다면, 모든 class의 확률 중 가장 높은 값을 갖는 class에 $x$가 속한다고 판단하겠죠? 가령, $ P(G = 1 | X = x) > P(G = 2 | X = x) $ 라고 한다면, $x$는 class 2 보다는 1에 속할 확률이 크다는 것이죠. 그렇다면, 이 두 확률이 같아지는 지점은 어떨까요? 이 지점은 class 1도 아니고 2도 아닌 애매한 `경계`가 됩니다. 즉, 우리는 주어진 자료에 대해 아래의 식을 풀며 두 class간의 `경계`를 구할 수 있게 됩니다.
$$ P(G = 1 | X = x) = P(G = 2 | X = x) $$
뒤에있을 계산의 편의를 위해 log비로 위의 식을 다시 나타내면 아래와 같이 됩니다.
$$ log(\frac{P(G = 1 | X = x)}{P(G = 2 | X = x)}) = 0$$
이제 구체적으로, 앞서 가정한 class $k$의 $X$에 대한 분포인 `다변량 정규분포` $f_k(x)$와 class $k$에 속할 `(사전)확률`인 $\pi_k$를 이용하여 `Bayes' Rule`을 적용하면 위의식은 다음과 같이 전개됩니다.
$$ log(\frac{P(G = 1 | X = x)}{P(G = 2 | X = x)}) = log(\frac{f_1(x)}{f_2(x)})+log(\frac{\pi_1}{\pi_2}) = $$
$$ {-\frac{1}{2}}x^T(Σ_1^{−1}−Σ_2^{−1})x+x^T(μ_1Σ_1^{−1}+μ_2Σ_2^{−1})−{\frac{1}{2}}(μ^2_1Σ_1^{−1}−μ_2^2Σ_2^{−1})+{\frac{1}{2}}ln{\frac{|Σ_2|}{|Σ_1|}}−ln{\frac{ \pi_2 }{\pi_1}}=0$$
여기서 `공분산이 같으면` $ Σ_1 = Σ_2 = Σ $, `quadratic form`인 $ x^T(Σ_1^{−1}−Σ_2^{−1})x $를 포함하여 `정규화 인자`를 `무효화` 시킵니다. 이를 통해 `선형` 결정 경계를 갖게됨을 암시합니다. 아래를 통해 확인하죠.
$$ log\frac{\pi_1}{\pi_2} - \frac{1}{2}(\mu_1+\mu_2)^T\Sigma^{-1} (\mu_1-\mu_2) + x^T \Sigma^{-1} (\mu_1-\mu_2) = 0$$
다변량 정규분포
$$f_k(x) = {\frac{1}{(2π)^{p/2}|Σ_i|^{1/2}}}e^{−1/2(x−μ_i)^TΣ_i^{-1}(x−μ_i)}$$
현실에서는 모수를 알 수 없음으로, 주어진 자료를 통해 아래를 구한 뒤 적용해야 합니다.
$\hat{\pi} = N_k/N$
$\hat{\mu_k} = \Sigma_{g_i=k}{x_i/N_k}$
$\hat{ \Sigma } = \Sigma_{k=1}^K\Sigma {g_i=k}(x_i - \hat{\mu_k}) (x_i - \hat{\mu_k})^T/(N-K)$
Quadratic Discriminant Analysis
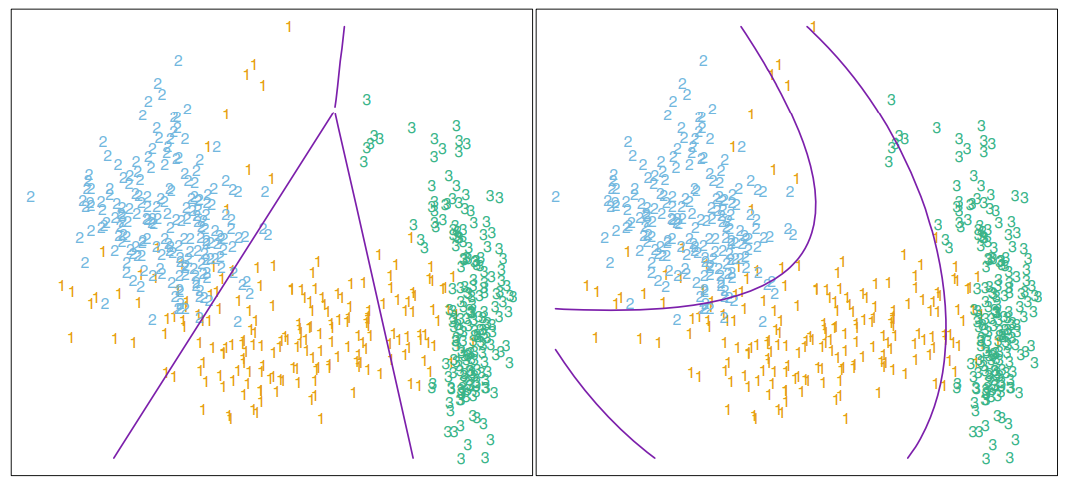
공분산을 가정하지 않는 경우, $x$에 대한 Quadratic term이 남아 계산이 힘들었습니다. 이렇게 나온 경계면 역시 사용이 가능한데, `곡선의 형태`로 경계가 생기게 됩니다. 이러한 방법을 `Quadratic Discriminant Analysis (QDA)`라고 합니다. 때에 따라서는 QDA를 통해 보다 세세한 분류를 하게될 수 도 있으며, QDA 과적합으로 인해 LDA를 섞어 쓰는 절충안(RDA)을 사용해야 할 수 있습니다.
Dimensionality Reduction
만약 차원 축소를 위해 `LDA`를 사용한다면, `클래스 간 분산을 최대화`하고 `클래스 내 분산을 최소화`하는 방향을 찾는 것이 핵심입니다. 이 방향은 수학적으로 다음과 같은 절차를 통해 구할 수 있습니다.
먼저, 각 클래스 $k$에 대한 평균 벡터 $\mu_k$와 전체 평균 벡터 $\mu$를 계산합니다. 클래스 평균 벡터는 해당 클래스의 데이터 포인트 평균으로 정의되며, 전체 평균 벡터는 전체 데이터의 평균으로 계산됩니다.
$$ \mu_k = \frac{1}{N_k} \sum_{i \in C_k} x_i, \quad \mu = \frac{1}{N} \sum_{i=1}^N x_i $$
다음으로, 클래스 간 분산 행렬 ($S_B$)과 클래스 내 분산 행렬 ($S_W$)을 정의합니다. 클래스 간 분산 행렬은 클래스 평균 간의 분산을 나타내며, 클래스 내 분산 행렬은 각 클래스 내부 데이터의 분산을 나타냅니다.
$$ S_B = \sum_{k=1}^K N_k (\mu_k - \mu)(\mu_k - \mu)^T $$
$$ S_W = \sum_{k=1}^K \sum_{i \in C_k} (x_i - \mu_k)(x_i - \mu_k)^T $$
LDA는 이 두 행렬의 비율을 최대화하는 방향을 찾습니다. 이제부터는 쉽습니다. `PCA`에서 공분산 행렬에 하는 것처럼, $S_W^{-1} S_B$ 행렬에 `고유값 분해`를 적용하여 고유값 ($\lambda$)과 고유벡터 ($w$)를 구합니다.
$$ S_W^{-1} S_B w = \lambda w $$
여기서, 가장 큰 고유값에 해당하는 고유벡터가 데이터의 주요 사영 방향(차원 축소 축)을 나타냅니다. 만약 여러 차원으로 축소하려면 상위 $m$개의 고유값에 대응하는 고유벡터를 선택합니다. 이렇게 선택된 고유벡터를 행렬 $W$로 구성하면, 차원이 축소된 새로운 데이터 $X'$는 다음과 같이 계산됩니다. $$ X' = XW $$ 이 과정에서 $W$는 $p \times m$ 크기의 행렬로, 원본 데이터 $X$를 $m$-차원으로 변환하는 역할을 합니다. 결과적으로, 사영된 데이터는 저차원 공간에서 클래스 간의 분리가 최대화되도록 변환됩니다.
Outro
1. LDA의 결정 경계면과 사영축은 반드시 직교하지는 않습니다.
2. LDA는 사실 `MANOVA` 기법과 밀접한 연관성이 있습니다. 시간이 허락된다면, 해당 부분에 대해서도 다루도록 하겠습니다.
3. LDA를 활용한 `유전자 마커 선택` 기법도 있습니다. 이 방법도 시간이 된다면 `Bioinformatics` 관련 카테고리에서 소개하도록 하겠습니다.
4. `분류`의 베이즈 룰 전개 과정과 `차원축소`의 $S_B$와 $S_W$를 보면 유사한 항이 보입니다. `분산관련된 항`으로 이 부분 때문에 두 가지 모두 `LDA`로 묶이는게 아닌하는 생각이 듭니다. 부족한 수학 지식으로 유추 뿐입니다... 혹, 명쾌하게 설명가능 하다면 제게 알려주세요!
감사합니다.
References
Book, "The Elements of Statistical Learning" (한국어판 책에 수식의 부호에 오류가 있으니 조심하세요!)
'통계 & 머신러닝 > 군집화' 카테고리의 다른 글
| [WGCNA] 주요 유전자 파악 및 모듈 평가 (2) | 2024.08.19 |
|---|---|
| [WGCNA] 유전자 군집화 (0) | 2024.08.19 |
| [WGCNA] 유사도 네트워크 계산 (0) | 2024.08.14 |
| [WGCNA] 기본 개념 (0) | 2024.08.14 |
