Gene Set Enrichment Analysis

`Gene Set Enrichment Analysis (GSEA)`는 `In Silico``pathway` 분석 기법으로, `microarray`나 `RNA-seq` 자료를 통해 특정 `gene set`이 관심있는 `표현형`과 얼마나 연관성이 있는지 확인하는 통계적 기법입니다. 여러 전통적인 기법과`PAEA`와 같은 새로운 방법의 검정법 등이 논문에 많이 그리고 새로이 등장하고 있습니다. 그 중 `GSEA`는 독보적인 위치에 있습니다. 그 이유로`GSEA`가 단순한 기술적 선점효과 뿐 아니라, 굉장히 단순하여 이해하기 쉬움으로부터 오는 해석력까지 갖추고 있기 때문으로 보입니다. 이번 포스트 에서는 그 원리를 한번 확인해보겠습니다.

Enrichment Score

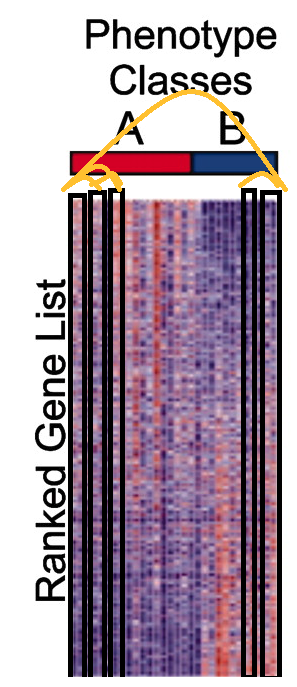
먼저 전체 유전자 pathway를 두 그룹에 대해 차이가 많이 나는 순서대로 줄 세웁니다. 주로 `(log) fold change`, `t-statistics` 또는 `correlation coefficient`등을 이용합니다. (본 논문에서는 `correlation coefficient`이용)

그리고 관심있는 유전자 집합이 그 중 어디에 위치해 있는지 살펴봅니다.

이 그림과 같이 가운데를 기준으로 위에 `쏠려` 있다면 (`enrich` 되어있다면), gene set이 phenotype과 방향에 따라 양 또는 음의 상관성이 있을것으로 예상 가능합니다. 그렇다면 이를 어찌 수치적으로 표현 가능할까요?

먼저 앞서 줄 세우기 위해 구한 `correlation coefficient`를 이용할 것입니다. 구체적으로 그 값과 함께 pathway와 관심 유전자 집합을 보자면 아래와 같이 되겠지요. (참고로 여기서 쏠려있는 관심 유전자의 무리를 `leading edge` 라고 합니다)

앞의 그림에서 바를 가로로 눞혀 놓았다. 가로의 바가 전체 gene 이고 correlation with phenotype으로 정렬되어있는 상태로, 아래의 그래프가 correlation의 정도를 나타내고 있다.

이제부터, 가로로 눞혀져있는 pathway를 왼쪽부터 오른쪽 끝 까지 한걸음 한걸음 훑으며 `걷겠습니다`. 걷는 중 전체 pathway에서 우리의 관심있는 유전자를 만나면, `hit` 그렇지 않다면 `miss`하게 됩니다. `hit`을 할 때마다 어떤 값을 양의 방향으로 더합니다. `miss`하게되면 반대 방향으로 어떤 값을 빼게 됩니다. 이 과정을 `random walk`라고 합니다.

Random walk중 hit하면 그 값이 위로 솟고, miss 할 때마다 아래로 꺼진다.

`Random walk`를 통해 계산되는 값 중 `hit`는 그룹에 대한 가중치(여기서는 correlation coefficient)를 정규화 한 값을 사용함으로 다 더하면 1이 나오게 됩니다. 반면 `miss`는 가중치를 사용하지 않고, 빈도수를 기준으로 유전자마다의 균일한 값을 할당 합니다. 이런 방식으로 위의 그림에서 빨간 `random walk`가 그려지게 됩니다.

이를 통해 `GSEA`는 `Enrichment Score (ES)`값을 구하게 됩니다. `ES` 값은 `쏠린 정도`를 정량화 한 수치로 `random walk`시 중심으로부터 가장 멀리 떨어져 있는 그 거리를 의미합니다. 아래의 그림처럼 `leading edge`가 초반에 등장한다면, 먼저 위로 가중치들이 쌓여 양으로 높은 값이 `ES`로 계산 되겠지요. 반대로, 관심있는 `gene set`이 pathway상 후반에 쏠려 등장한다면 `miss`가 그 전까지 지속되어 균등하게 아랫 방향으로 쌓여 음의 방향으로 높은 값이 `ES`로 계산 됩니다.

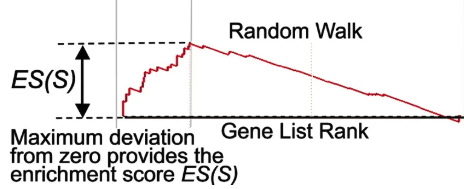
`ES`는 정규화 된 값을 계산하여 1과 -1 사이의 값을 갖게되며, 아래와 같이 식으로 표현 가능합니다.

$$ P_{hit}(S,i)=\sum_{g_j\in S, j\leq i}\frac {|r_j|^p} {N_R}, where N_R=\sum_{g_j\in S}|r_j|^p $$

$$ P_{miss}(S,i)= \sum_{g_j\in S, j\leq i}\frac {1} {N-N_H} $$

The ES is the maximum deviation from zero of $P_{hit} – P_{miss}$.

Kolmogorov-Smirnov statistic

이러한 `ES`의 통계량은 cumulative density를 사용한 일종의 변형된 Kolmogorov-Smirnov (KS) statistic입니다. 만약 $P_{hit}$에 $P_{miss}$처럼 weight를 사용하지 않고, 단순빈도를 사용한다면 original KS statistic과 값이 같아집니다.

유의성 검정

그렇다면, 유의성은 어떻게 파악할까요? `GSEA`에서는 `permutation test`를 기반으로 통계적 유의성을 판단합니다. 여기서 두가지 방법이 있는데, 표본의 수가 충분하지 않다면 유전자의 위치를 섞음으로 영분포를 생성합니다.

Permutation test

Permutation test는 간단히 말해서 현재 관측된 현상이, 우연적인 상황(영분포)을 가정했을 때 얼마나 극단적인 경우인지 확인하는 비모수적 통계 검정입니다. 영분포를 생성하기 위해서 label을 섞어(`permutation`하여) 동일한 방식으로 통계량을 계산합니다. 보통 1000번 이상 다른 랜덤 시드를 통해 섞어 영분포를 만듭니다. 생성된 영분포를 기준으로 관측된 현상의 위치부터 오른쪽(또는 왼쪽) 꼬리까지를 적분하면 `p-value`가 나오게 됩니다.