ZIBseq

Intro

  `Microbiome data` 분석 역시 그룹간 유의미하게 다른 microbiome을 찾는것이 정말 중요합니다. 참고로 Differentially Expressed Genes (DEG) 를 찾는 과정과 매우 유사하며, microbiome자료 에서는 유의미하게 다른 microbiome을 주로 Differential Abundance Features (DAFs) 라고 부른다. Microbiome data는 `ASV`나 `OTU`를 사용하는데, 결국 tabluar count data이기 때문에 기존의 RNAseq 분석 방법과 크게 다르지 않다 생각할 수 있습니다. 때문에 이전 포스터에서 소개한 `edgeR`과 `DESeq2`도 `DAFs`를 찾는데 사용이 가능하지만, `microbiome`의 생물학적 특성에 맞는 다른 여러 방법들이 새로이 제시되고 있습니다. 이번에 소개할 `Zero-Inflated Beta Regression for Differential Abundance Analysis with Metagenomics Data (ZIBseq)` 이 그러한 방식 중 하나입니다.

 

ZIBseq paper

 

  Citation이 아주 많지는 않지만, 단순히 자료형만을 고려하는 것을 넘어서 실제로 생물학적 특성을 고려하는 방식중 가장 직관적이라 생각되어 가져오게 되었습니다. 그리고 더 구현 될 만한 내용들이 있어서 추가로 구현한 내용을 `github`에다가 pull request 보내었으니, 혹시 확인해보고 틀린부분이 있으면 알려주길 바랍니다.

 

ZIBseq

  사람의 몸속에는 100조개 정도의 미생물이 같이 살고있습니다. 하지만 체내의 source는 `제한적`이라, 한 종의 microbiome의 thrive는 다른 여러 종의 microbiome의 decline을 의미합니다. 때문에 microbiome data는 RNAseq data와는 다르게 dominance를 고려해야합니다. 수학적으로 보면 `sum to one constraint`가 걸려있는 셈입니다. `ZIBseq`은 이러한 이유로 microbiome을 `beta 분포`로 가정합니다. 

 

  `Normalization`은 `Relative Abundance (RA)`로 정말 직관적입니다. 값을 각 sample의 depth (sample의 total count) 로 나누어 0 ~ 1 의 `proportion`으로 나타냅니다. 하지만 단순히 RA를 적용하기에는 자료 특성상 0 또는 0에 매우 가까이 적은 값이 너무 많이 등장하게됩니다. 이렇게 극단적인 `left skewed` 자료는 beta 분포를 가정하기에는 적절치 않습니다. 때문에 이 논문에서는 여기에 `square root` 또는 `cube root transformation`을 적용하여 문제를 해소합니다.

 

  핵심이 되는 모형은 제목에서 알 수 있듯이 `beta regression`에 `mixed model`을 사용합니다. `Beta` 분포 역시 Poisson & NB처럼 다양한 관점으로 parameter를 잡을 수 있습니다. 여기서는 $x$가 변환까지 된 microbiome data일 때에 $x \sim beta(\mu, \phi)$ 이며, $\mu$와 $\phi$는 각각 `mean`과 `precision parameter`라고 하는데, 가장 대중적인  $x \sim beta(\alpha, \beta)$ 와는 다른 모습입니다. 각각 다른 접근 방식에서 parameter의 관계는 아래와 같습니다. 

 

$$\mu = {\alpha \over {\alpha + \beta}}$$

$$\phi = \alpha + \beta$$

$$\rightarrow E(x) = \mu \; and \; Var(x) = {{\mu(1-\mu)} \over {1 + \phi}}$$

 

  $\phi$는 고정된 값 $\mu$에 대하여 더 큰 값을 갖을수록, 더 작은 $Var(x)$를 갖으므로 `precision parameter`라고 합니다. 이렇게 parameter를 잡는 이유는 잘 모르겠지만, 기존의 $\alpha, \beta$ `shape parameter`보다 `mean`과 `variance`의 관점에서 보고 싶어서 사용하는게 아닌가 싶습니다.

 

  이 논문에서는 이 두가지 parameter 말고도 하나의 parameter $\alpha$ (shape parameter가 아님!! 논문에서 사용한 notation 그대로 가져오느라 중복처럼 되버림)를 더합니다. $\alpha$는 $x=0$일 확률로 `mixed model`의 factor라고 생각하면 된다. 이에 따라 mixture density는 $f(x;\mu,\phi)$가 beta density인 경우 아래와 같이 됩니다.

 

$$Bi(x;\alpha, \mu, \phi)= \begin{cases} \alpha & \text{if }x=0 \\ (1-\alpha)f(x;\mu,\phi) & \text{if } 0<x<1 \end{cases}$$

 

  이 논문에서는 sample과 feature의 index를 각각 아랫 첨자와 윗 첨자로 나타냅니다. 가령, 변환된 $i^{th}$ sample의 $j^{th}$ feature는 $x_i^{(j)}$로 notation을 사용합니다. 이 논문에서는 sample과 feature의 각각 상징되는 알파벳은 $i$와 $j$이다, 그리고 parameter $\rho,\:\beta$의 아랫첨자는 샘플에 관한것이 아니라 단순히 identification에 관한 것이므로 신경 쓰지 말자. 이러한 notation에 대한 정보와 mixture density를 생각하면, $j^{th}$ feature에 대한 data는 아래와 같이 모델링 될 수 있다.

 

$$ logit(\alpha_i^{(j)}) = \rho_0^{(j)}, \quad logit(\mu_i^{(j)}) = \beta_0^{(j)} + \beta_1^{(j)}y_i $$

 

  여기서 $y$가 바로 그룹에 대한 indicator variable이며, 때문에 코드를 돌리기 전 꼭 group variable이 factor 처리가 되었는지 확인 해야합니다. 다음 수순으로 자연스럽게 귀무가설 $H_0:\:\beta_1^{(j)} = 0$에 대한 test를 진행합니다. 이렇게 모든 feature에 대한 모델링과 검정이 완료되면, 그 수 만큼 p-value가 나오게 됩니다. 마지막으로, ZIBseq에서도 역시, `Benjamini-Hochberg` 방법으로 `FDR correction`을 적용하여 결과 q-value를 냅니다. 많이들 multiple testing correction을 한 뒤의 p-value를 q-value라고 하니 알아두면 이해하는데 편하다. 

 

  결과로 simulation study와 real data analysis를 다른 여러 방법들과 비교하며 제시합니다. Simulation에서는 `Zero-inflated Gaussian (ZIG)` 와 `ZIBseq`을 비교하는데, 대부분의 자료 분포와 parameter setting에서 `ZIBseq`이 실제로 유의미하게 만들어 놓은 feature를 더 잘 찾는다는 (AUC가 높다는) 이야기를 합니다. Real data analysis에서는 obesity data를 사용했는데 기존에 잘 알려진 microbiome을 잘 선택한다는 이야기를 합니다. 그룹이 총 4가지로 Body Mass Index (BMI)를 기준으로 나눕니다. Normal(N), Overweight(O), Obese(OB), 그리고 Morbidly Obese(OM) 순으로 뚱뚱한 것. 여기서는 두 그룹간의 차이만 구현되어 있음으로 `N + O + OB vs. OM` 으로 나누어 검정을 진행 했습니다. 

 

Real data analysis에서 선택된, 그리고 잘 알려진 obesity에 관련된 microbiome boxplot.

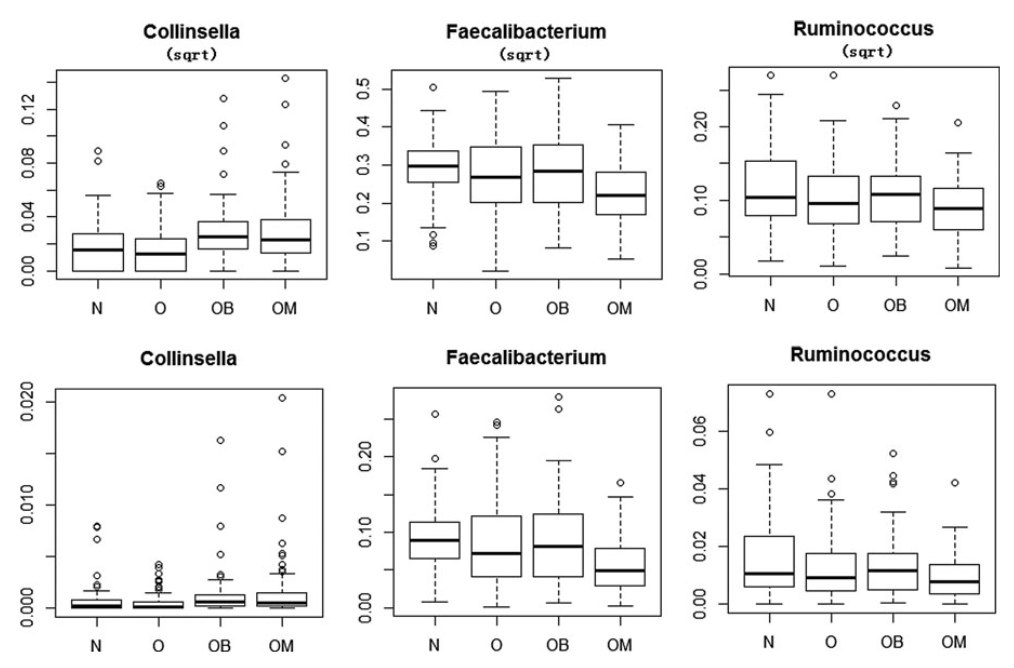
구현되면 더 되면 좋았을 부분들

Covariate adjustment

  중심이 되는 모형을 자세히 보면, 결국 group 변수만 independent variable로 사용되도록 디자인 되어 있습니다. 이렇게 되면 문제가, phenotype에 대해 주요한 영향을 끼치는 clinical variable의 잡음 또는 변량을 (covariate) 보정 못 하게 됩니다. 때문에, 온전한 independent variable의 response variable에 대한 효과를 검정 할 수 없게 되어 결과를 신뢰하지 못 하게 될 수 있습니다. 여러 방식이 있겠지만, 가장 간단하게 independent variable에 covariate도 같이 사용하여 문제를 해소 하였습니다. 아래의 식에서 $z$는 하나의 clinical variable입니다.

 

$$ \quad logit(\mu_i^{(j)}) = \beta_0^{(j)} + \beta_1^{(j)}y_i +\beta_2^{(j)}z_i $$

 

More than 3 groups

  Real data analysis에서도 알 수 있듯, 여러 그룹에 대한 검정은 불가하여 두 그룹으로 묶어서 진행합니다. 이렇게 되면 묶인 그룹 내에서의 차이를 볼 수 없게 되며, 어떤 경우 묶인 그룹간 차이가 커 또다른 묶인 그룹과 실제로 차이가 있음에도 차이가 없다고 결과가 나올 수 있습니다. 기존에 사용된 GAMLSS 패키지 내부를 뜯어보지는 못하여서 Wald인지 Score인지 어떠한 test statistic이 사용되었는지는 모르지만, 3그룹 이상의 상황을 위해서 dummy coding을 한 뒤 Likelihood Ratio Test (LRT)를 하도록 바꾸었습니다. 예를들어, row는 sample이고, column은 group에 대한 indicator라 할 때에 3그룹에 2명씩 속하는 6명의 dummy coding은 아래와 같이 표시할 수 있습니다. 결국 $3 - 1 = 2$ 의 자유도로 $H_0:\: \mu_1=\mu_2=\mu_3$ 에 대한 검정이 가능해집니다.

 

\begin{pmatrix} 0 & 0 \\ 0 & 0 \\ 1 & 0 \\ 1 & 0 \\ 0 & 1 \\ 0 & 1 \end{pmatrix}

 

Implementation

  위의 두가지 내용에 대하여 `Github`으로 implementation한 것을 pull request했습니다. Branch는 `multinomial`로 만들었습니다. 아래 링크를 달아 놓았으니 봐주시면 감사할 것 같습니다. Pull requset를 하고 얼마 안가서 R cran의 mirror로 read only라는 사실을 관리자가 알려왔습니다. 때문에 원작자와 maintainer에게 따로 메일로 수정 제안을 메일 보내었습니다. 오래 전 논문이고, 다른 일로 바쁘실테니 받아들여질 확률이 희박하겠지만, 수정되면 다른 포스터에 올리겠습니다.

https://github.com/codespermuted/ZIBseq/blob/multinomial/R/ZIBseq.R

ZIBseq/R/ZIBseq.R at multinomial · codespermuted/ZIBseq

구현 못한 내용들

Multiple testing correction, correlated features

  일반적으로 `Familywise Error Rate (FWER)` correction은 너무 보수적이라 대부분의 feature가 의미 없다 나옵니다. 특히 `Bonferroni correction`은 feature의 수가 조금만 많아져도 거의 다 날라갑니다. 때문에 `False Discovery Rate (FDR)` correction을 많이 진행합니다. 하지만, microbiome 자료는 위에서 말 했다시피 feature 서로 negatively correlated 되어 있습니다. 엄밀하게는 이런 correlation을 고려하여 `Benjamini-Hochberg (BH)` 말고  `Benjamini-Yekutieli (BY)` FDR correction을 적용 하는게 더 좋지 않을까 생각이 됩니다. BY 방법은 statistical power가 좀 낮다는 단점이 있지만.... Bioinformatics에서는 매우 높은 dimensionality를 갖고 분명 correlation이 있는 실험이 많은데, 거의 대부분 BY대신 BH를 사용합니다. 그 이유가 statistical power말고 내가 알지 못하는 다른 치명적인 단점이 있을 수도 있어 이 부분은 개선을 위한 코드로 구현지는 못 하였습니다. 물론 그냥 statistical power와 correlation 고려하는 것을 교환한 것일 수도 있다.

Ordinal group version

  그 외에도 real data analysis의 그룹과 같이 `ordinal` group variable에 대하여는 이러한 `multinomial` 방법보다, 다른 `ordinal` 방법을 사용하는 것이 더 좋습니다. `Ordinal`로 group variable을 보면 testing시 `Degree of Freedom (DF)` 가 1로 줄어들어 `statistical power`가 커지기 때문죠. 하지만, negatively correlated 된 특성을 잘 보존하면서 group variable을 ordinal로 보려면 모형이 아예 바뀌거나, 모형은 유지하되 group variable을 그냥 같은 interval을 갖는 integer로 취급하여 진행하여야 가능한 이야기입니다. 구현하는데 큰 문제는 없지만, 결과가 옳은지 검증이 불가하여 구현에 염두하지는 않았습니다.

Outro

  `ZIBseq`은 쉽고 직관적인 방식의 DAFs 찾는 방법이였습니다. 분명 좋은 방법이라고 생각합니다. 하지만 어떤 이유에서인지 citation이 매우 낮습니다. 과연 어떤 지표가 논문의 질을 판단하는데 도움이 될까요? 조금 더 근본적으로 가게되면 'Motivation은 매우 직관적이고 실제 microbiome의 negatively correlated 특성을 잘 반영했지만, 과연 이 방법이 real world를 가장 많이 설명하는 방식일까?' 하는 질문까지 도달하게 됩니다. 오직 하나님만이 이 질문에 대한 정답을 아시지 않을까 싶습니다. 내 수준에서 적어도 괴상한 방식은 잘 거를 수 있도록 또는 더 잘 판단 할 수 있도록 공부를 계속 해야겠습니다. 이런 맥락에서 구현 못한 두가지 issues에 대해 무엇이든 좋으니 의견이 있으면 꼭 알려주길 바랍니다.

출처

https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6109378/

Zero-Inflated Beta Regression for Differential Abundance Analysis with Metagenomics Data - PMC